Solving the Crocodile Math Problem in R

Posted on October 19, 2015

Using R to solve the crocodile math problem from the Scottish Higher Maths exam of May 2015.

Motivation

Reading the Spanish newspaper La Vanguardia, I found a curious article about a math problem that S4 Scottish students (the equivalent of high school’s senior year) struggled with last May on their SQA Higher Maths test.

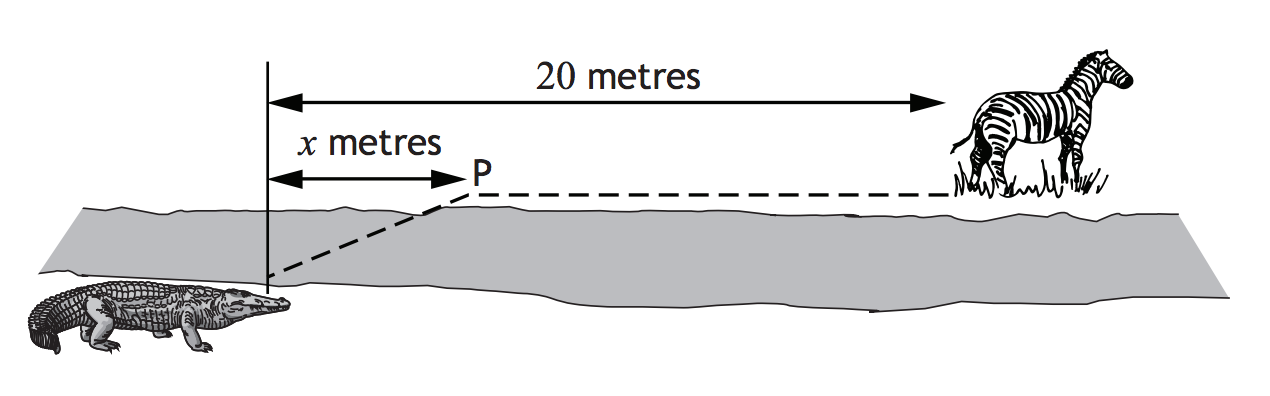
Here’s the problem.

Getting Started

The first thing to do is write a function containing the formula of \( T(x) \) the time taken for the crocodile to reach its prey:

# time taken function
croctime <- function(x) 5 * sqrt(36 + x^2) + 4 * (20 - x)

Now let’s look at this function. I’ll choose an interval of (0, 20) for \( x \) since this represents the distance (0 meters, 20 meters).

curve(croctime, 0, 20, las = 1, lwd = 5, col = "#68A959",
      xlab = "distance", ylab = "time")

First question

Calculate the time taken if the crocodile does not travel on land. That means that the crocodile swims the entire 20 meters.

croctime(20)

## [1] 104.4031

Second question

Calculate the time taken if the crocodile swims the shortest distance possible. Personally I think that this question is poorly written and/or bad designed. What does the “shortest distance possible” mean? Assuming that the shortest distance possible is 0 meters, then the time taken to swim 0 meters is:

croctime(0)

## [1] 110

Third question

Between these two extremes there is one value of \( x \) which minimizes the time taken. Find this value of \( x \) and hence calculate the minimum possible time. This is a typical calculus problem of minimizing a function. In this case the function to be minimized is the time taken. This implies calculating the derivative of \( T(x) \).

We can use the function deriv() to compute the derivative of a simple expression (symbolically).

# derivative of T(x)
deriv(y ~ 5 * sqrt(36 + x^2) + 4*(20 - x), "x")

## expression({
##     .expr2 <- 36 + x^2
##     .value <- 5 * sqrt(.expr2) + 4 * (20 - x)
##     .grad <- array(0, c(length(.value), 1L), list(NULL, c("x")))
##     .grad[, "x"] <- 5 * (0.5 * (2 * x * .expr2^-0.5)) - 4
##     attr(.value, "gradient") <- .grad
##     .value
## })

As you can tell from the output of deriv(), the fifth line contains the desired derivative: .grad[, "x"] <- 5 * (0.5 * (2 * x * .expr2^-0.5)) - 4

We can also obtain this derivative by using the function D() and pass it the body of the function croctime() like so:

g <- function(x) {}
body(g) <- D(body(croctime), 'x')

body(g)

## 5 * (0.5 * (2 * x * (36 + x^2)^-0.5)) - 4

Looking at the graphic of time, the curve has a minimum somewhere between 7 meters and 10 meters. We can evaluate the derivative g() with some x values to try to narrow down our search for the minimum value.

# distance values
seq(7, 10, length.out = 10)

##  [1]  7.000000  7.333333  7.666667  8.000000  8.333333  8.666667  9.000000
##  [8]  9.333333  9.666667 10.000000

# evaluating derivative
g(seq(7, 10, length.out = 10))

##  [1] -0.20371699 -0.13021350 -0.06247499  0.00000000  0.05767171
##  [6]  0.11096096  0.16025147  0.20589238  0.24820083  0.28746463

Aha! the minimum value is at a distance of 8 meters! To confirm that 8 is actually the root of the polynomial, we can use the function multiroot() from the package "rootSolve" by Karline Soetaert

library(rootSolve)

multiroot(g, c(7, 10))

## $root
## [1] 8 8
## 
## $f.root
## [1]  8.881784e-16 -3.693739e-10
## 
## $iter
## [1] 5
## 
## $estim.precis
## [1] 1.846874e-10

There you go: the minimum taken time for the crocodile to catch the zebra is given when the crocodile swims 8 meters, and then walks the other 12 meters.