Practice: Random Variables

1) Type of Random Variable

Choose a STAT 20 student at random. Decide whether each of the following is a discrete or continuous random variable:

  1. The number of courses the student takes this semester:

  2. The student’s weight:

  3. The student’s commute time (in minutes) to campus:

  4. The number of pets the student has:

  5. The (exact) time the student sleeps during a week:

  6. The number of caffeinated beverages that the student drinks in a typical week:

  1. Discrete
  2. Continuous
  3. Continuous
  4. Discrete
  5. Continuous
  6. Discrete


2) Tossing a fair coin

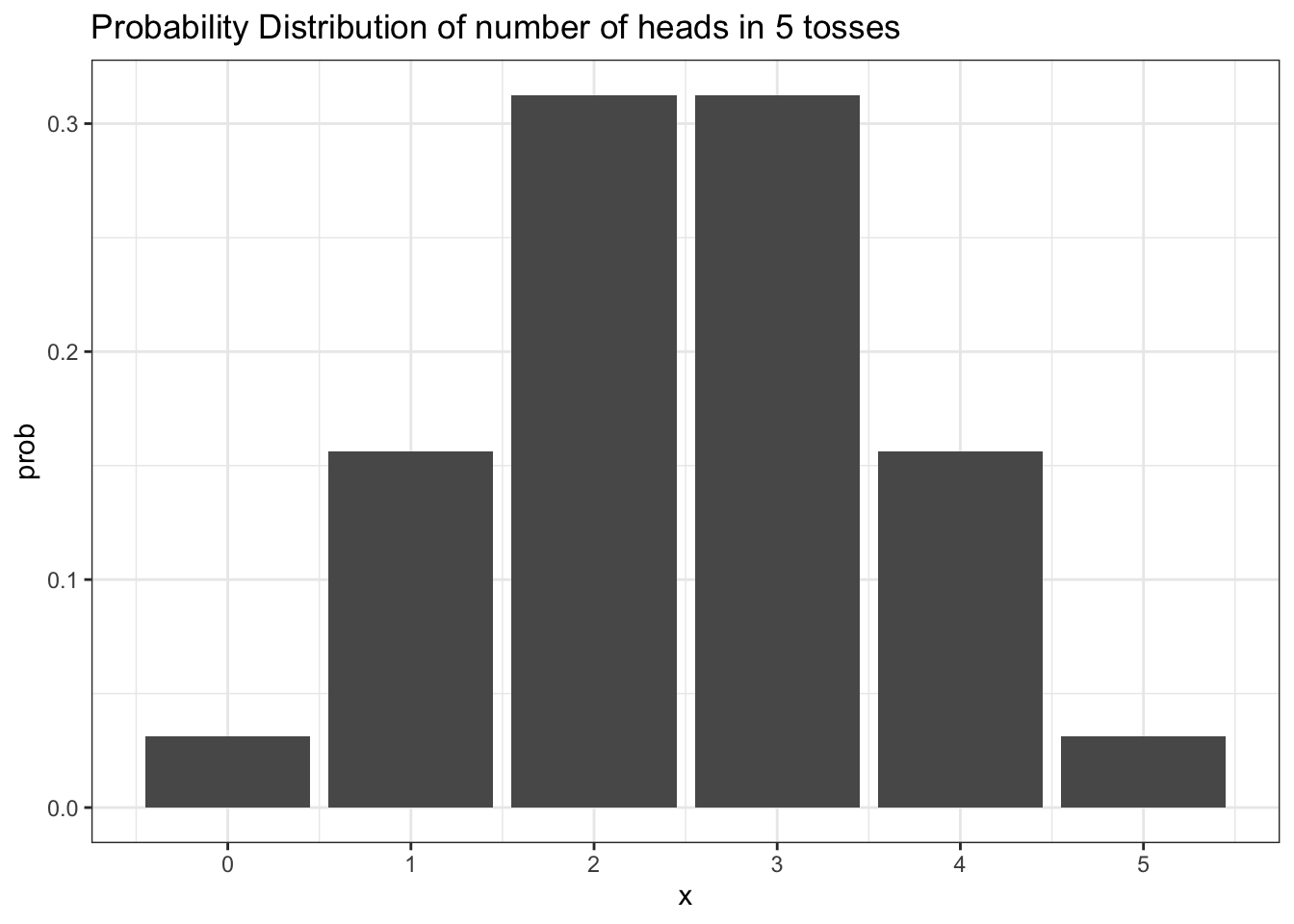
Let \(X\) be the number of heads in five tosses of a fair coin. We are interested in finding the probability distribution of \(X\), that is: \(P(X = k)\)

  1. What values will \(k\) take?

  2. Use dbinom() to find the probability distribution of \(X\). In other words, obtain the values of \(P(X = k)\) for all values of \(k\).

  3. Sketch a graph of the probability histogram of \(X\).

  4. Sketch a graph of the cumulative distribution function (cdf) \(F(x)\).

  1. \(k = 0, 1, 2, 3, 4, 5\)

  2. dbinom(x = 0:5, size = 5, prob = 0.5)

  3. Graph of the probability histogram.

Probability Histogram
  1. Sketch a graph of the CDF.

CDF


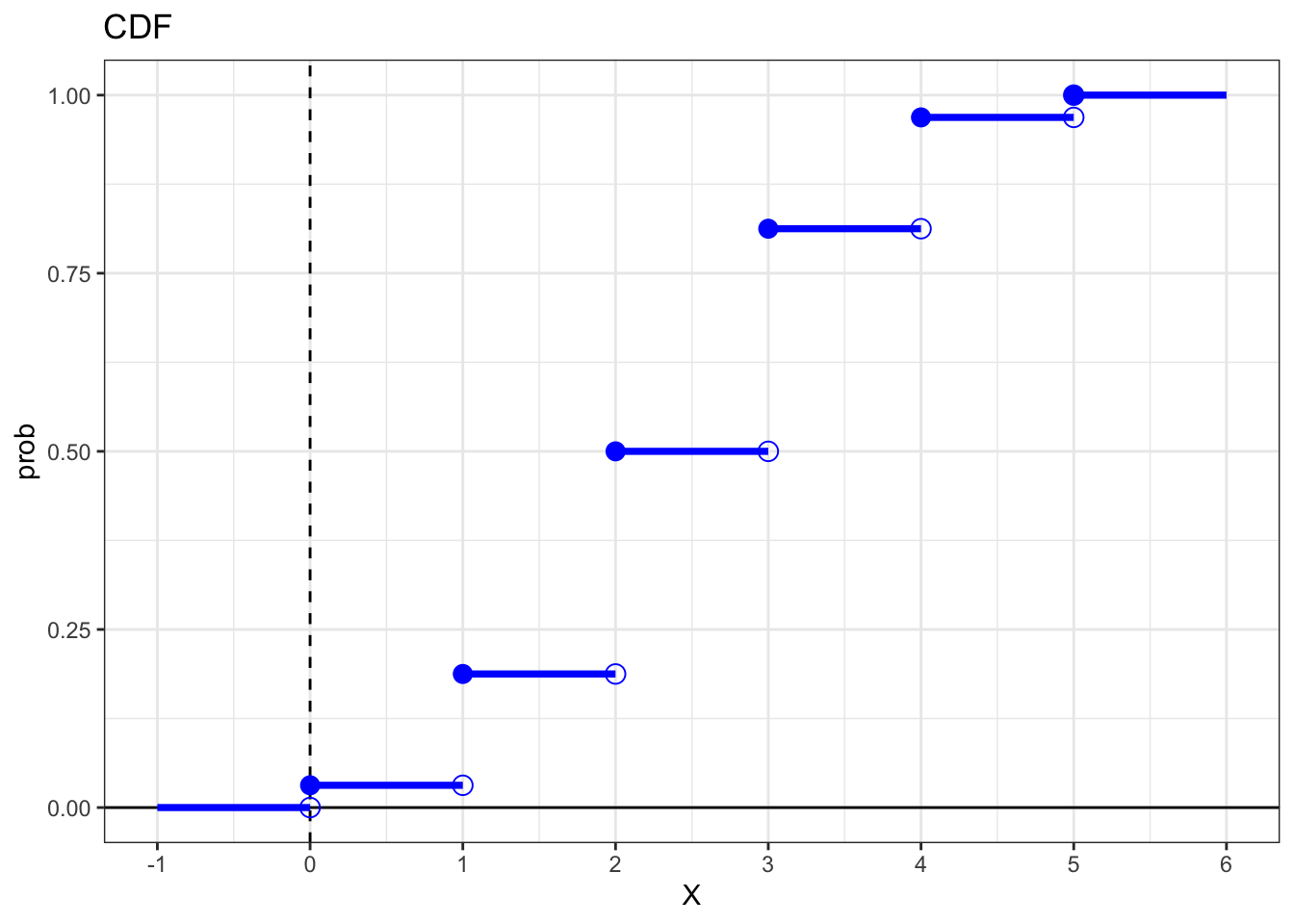
3) Tossing a biased Coin

Let \(Y\) be the number of heads in four tosses of a biased coin where the chance of heads is 3/5.

  1. Use dbinom() to find the probability distribution of \(Y\). In other words, write down the values of \(P(Y = k)\) for all values of \(k\).

  2. Sketch a graph of the cumulative distribution function (cdf) \(F(y)\).

  1. dbinom(x = 0:4, size = 4, prob = 3/5)

  2. CDF

CDF


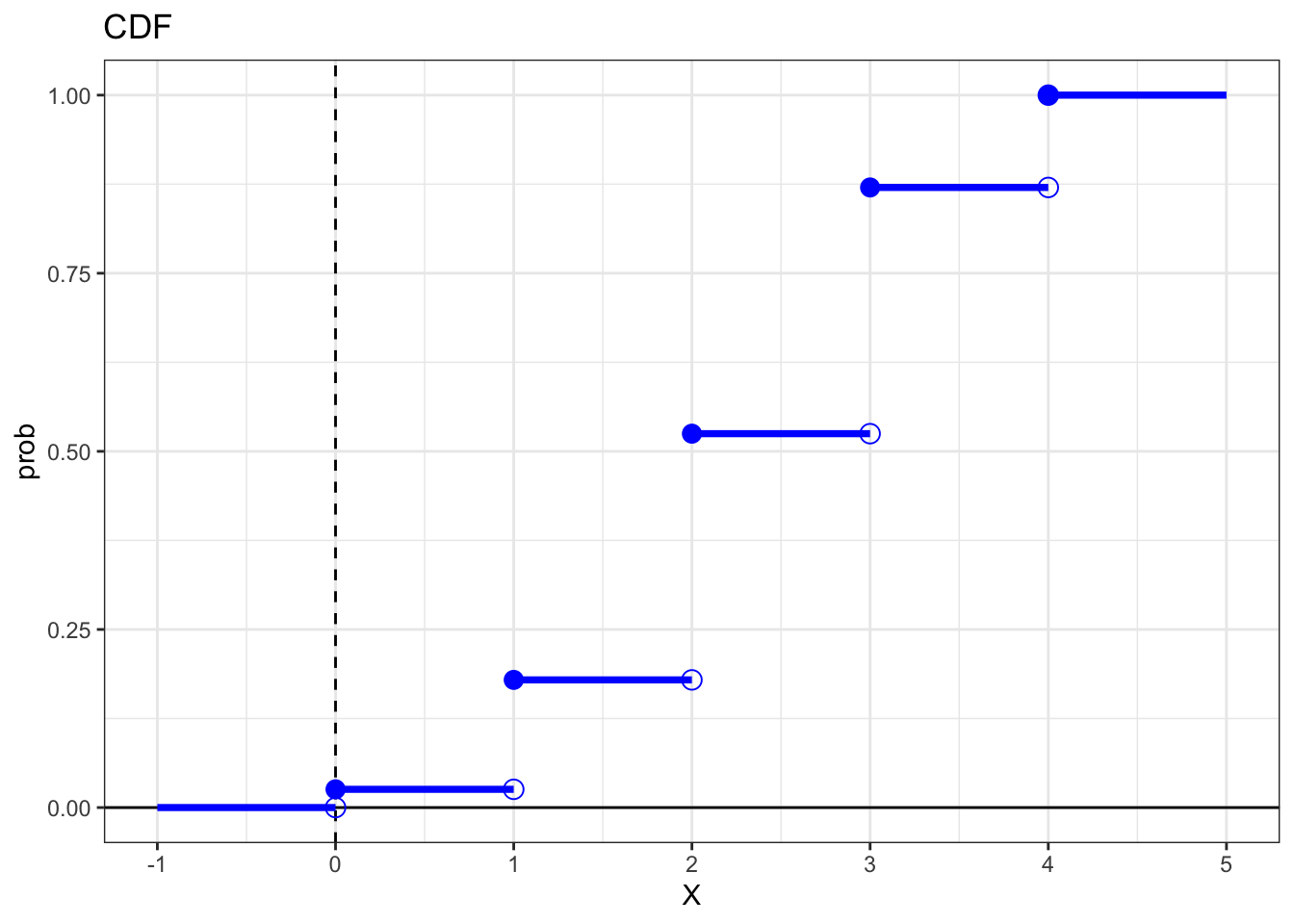
4) Deck of cards

Consider a deck of 52 cards. Suppose we are interested in the number of hearts dealt in a hand of five. Call this number \(Z\).

  1. Which of the following is the correct distribution of \(Z\)?

    1. Bernoulli
    2. Binomial
    3. Hypergeometric
    4. Poisson

  2. Based on your answer for part a), find the probability distribution of \(P(Z=k)\). Do this with the corresponding R function for the chosen distribution.

  1. option iii) Hypergeometric

  2. dhyper(x = 0:5, m = 13, n = 39, k = 5)

  3. CDF

CDF


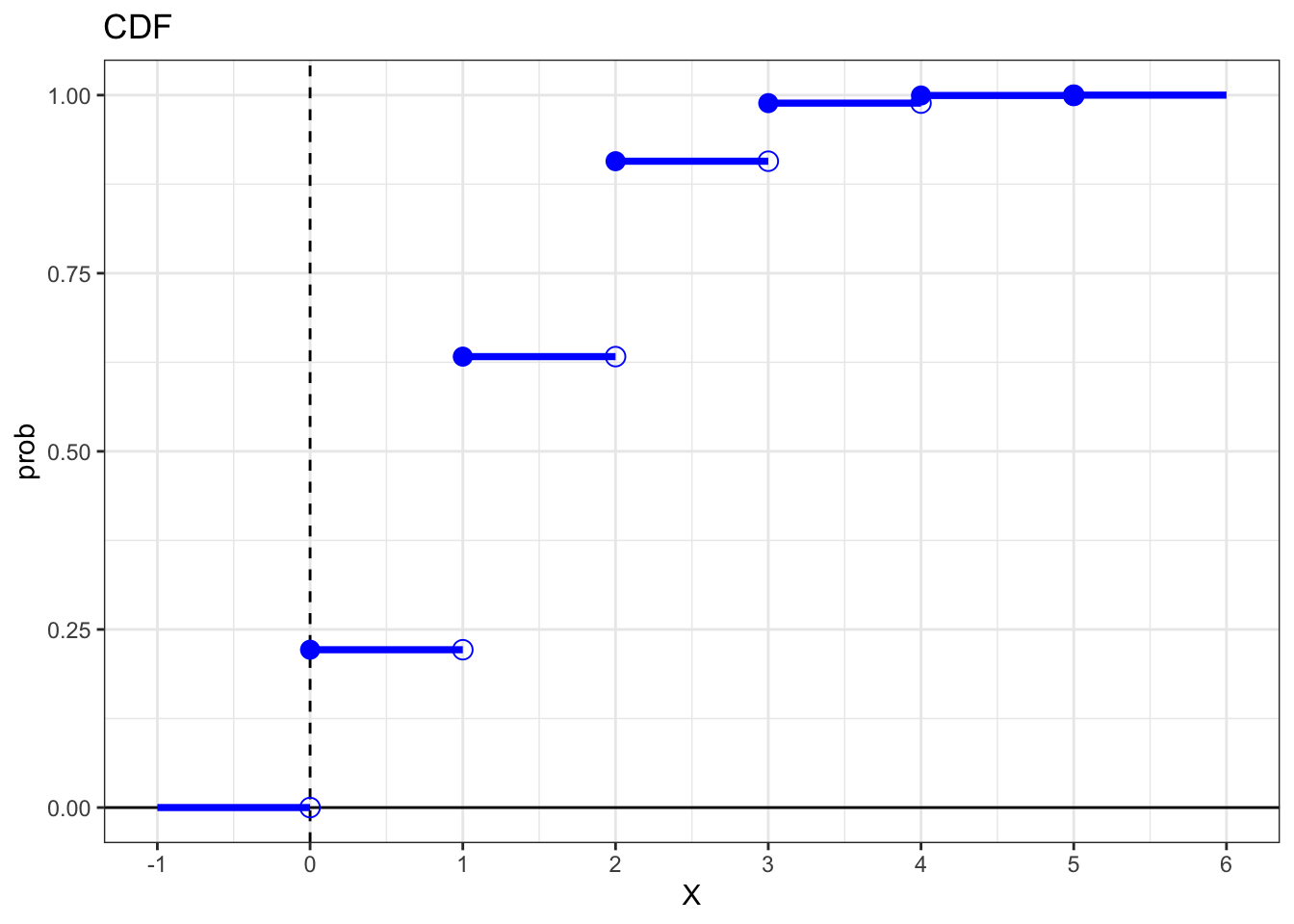
5) Rolling a pair of dice

Consider two colored 6-sided dice: one of them is a blue die, and the other is a red die. You roll the dice, and look at the numbers on their top faces. Let \(W\) be a random variable that takes the following values:

  • \(W = -1\) if the number in the blue die is less than the number in the red die.
  • \(W = 0\) if the number in the blue die is equal to the number in the red die.
  • \(W = 1\) if the number in the blue die is greater than the number in the red die.

For example, if the blue die lands 3 and the red lands 5, then \(W\) = -1. If both dice land 2, then \(W\) = 0. If the blue die lands 4 and the red lands 1, then \(W\) = 1.

Below is a sketch of the cumulative distribution function (cdf) \(F(w)\).

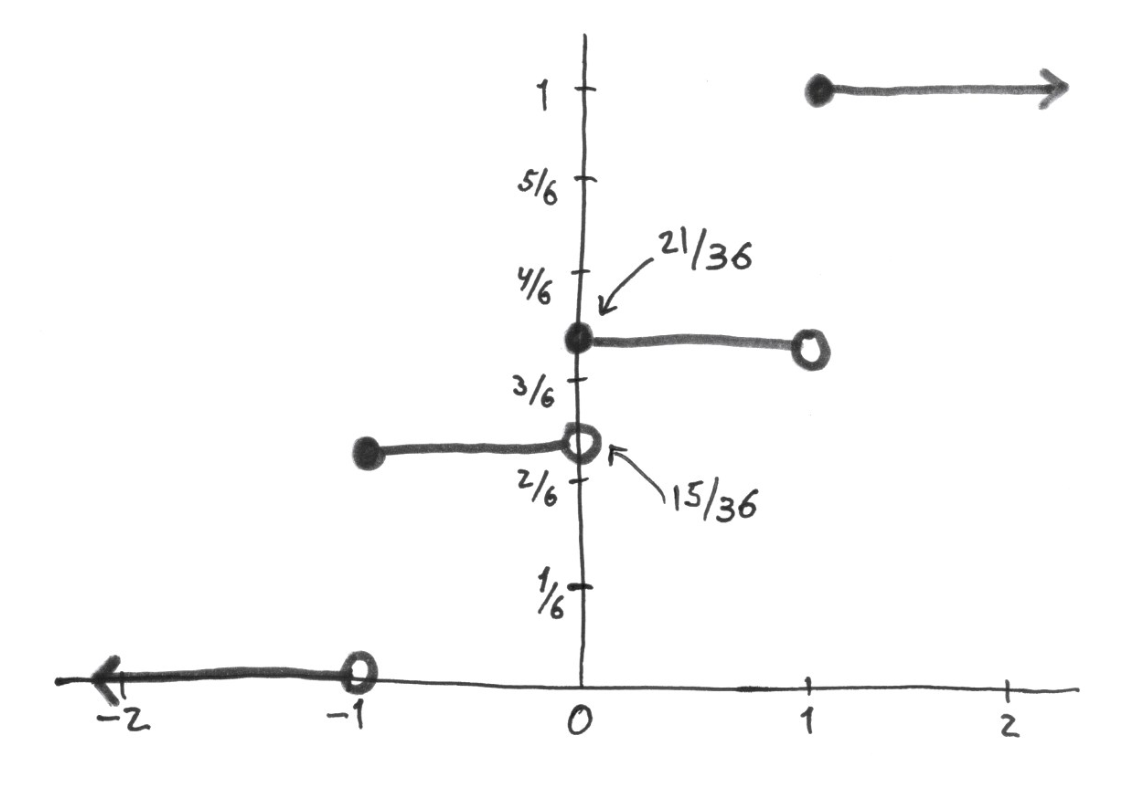
Based on \(F(w)\), find the probabilities:

  1. \(P(W = -1)\)

  2. \(P(W = 0)\)

  3. \(P(W = 0.5)\)

  4. \(P(W = 1)\)

  1. \(P(W = -1) = 15/36\)

  2. \(P(W = 0) = 21/36 - 15/36 = 6/36\)

  3. \(P(W = 0.5) = 0\)

  4. \(P(W = 1) = 1 - 21/36 = 15/36\)


6) Rolling a pair of dice (cont’d)

Refer to the colored dice of the previous problem. Let \(V\) be a random variable that takes the following values:

  • \(V = 0\) if both dice land on even numbers.
  • \(V = 1\) if both dice land on odd numbers.
  • \(V = 2\) if one die is even, and the other is odd (regardless of color).

  1. Find \(P(V = 0)\)

  2. Find \(P(V = 1)\)

  3. Find \(P(V = 2)\)

  1. \(P(V = 0) = 9/36\)

  2. \(P(V = 1) = 9/36\)

  3. \(P(V = 2) = 18/36\)