7.4 Mean as a Projection

We can gain insight to what a mean is doing if we regard a variable from the perspective of the individuals’ space. This interpretation is less common than the balancing point, but it is equally revealing and informative.

Consider the \(n\)-dimensional space \(\mathbb{R}^n\) illustrated in the figure below. In this space, each dimension is associated to an individual. The variable \(X\) is represented by the blue vector \(\mathbf{x}\). In turn, the orange vector represents the \(n\)-element unit-vector \(\mathbf{1}\). From this point of view, the mean acquires a very interesting meaning: it turns out that the mean is the measure of the projection of \(\mathbf{x}\) onto the axis spanned by the unit vector \(\mathbf{1}\).

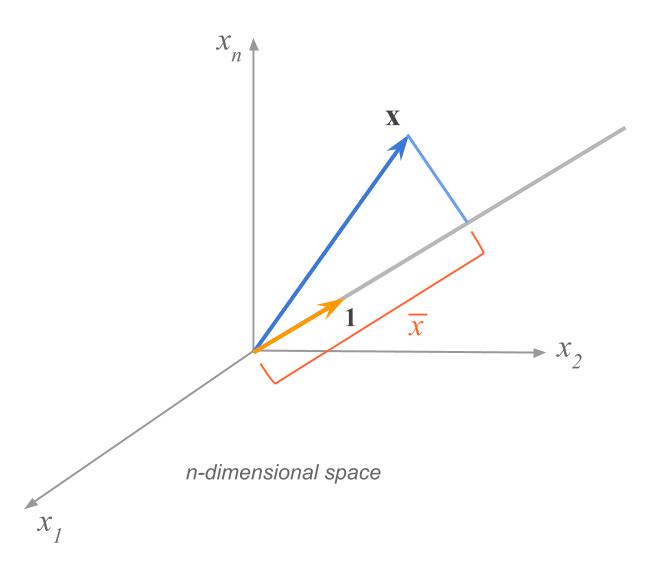
Figure 7.3: Mean as the measure of a projection

So what is the meaning of this orthogonal projection? It tells you that \(\bar{x} \mathbf{1}\) is the multiple of the unit-vector that is the closest to \(\mathbf{x}\) in the least squares sense:

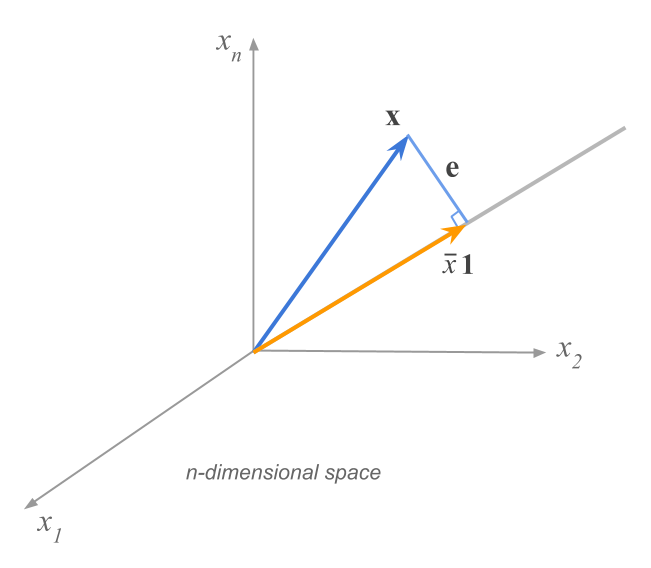
Figure 7.4: A variable and its mean vector

The size of the residual vector \(\mathbf{e} = \mathbf{x} - \bar{x} \mathbf{1}\) is the smallest among all other multiples of \(\mathbf{1}\) that you can use to approximate \(\mathbf{x}\).