2.3 Types of Matrices
There are various kinds of matrices which are commonly used in statistical learning methods. Let’s briefly revisit some of them.
2.3.1 General Rectangular Matrix
The most general type of matrix is a rectangular matrix. This means that there is an arbitrary number of \(n\) rows and \(p\) columns.
\[ \left[\begin{array}{ccc} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \\ 10 & 11 & 12 \\ \end{array}\right] \]
If a matrix has more rows than columns \(n > p\), sometimes we call this a vertical or tall matrix:
\[ \left[\begin{array}{ccc} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \\ 10 & 11 & 12 \\ 13 & 14 & 15 \\ \end{array}\right] \]
In contrast, if a matrix has more columns than rows, \(p > n\), sometimes we call this a horizontal, flat or wide matrix:
\[ \left[\begin{array}{cccc} 1 & 2 & 3 & 4 & 5 \\ 6 & 7 & 8 & 9 & 10 \\ 11 & 12 & 13 & 14 & 15 \\ \end{array}\right] \]
2.3.2 Square Matrix
A square matrix is one with same number of rows and columns, \(n = p\). In statiscal learning, various matrices derived from a data matrix are typically square, this usually happens when working with derived cross-products such as \(\mathbf{X^\mathsf{T} X}\) or \(\mathbf{X X^\mathsf{T}}\).
\[ \left[\begin{array}{ccc} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \\ \end{array}\right] \]
2.3.3 Symmetric Matrix
A symmetric matrix is a special case of a square matrix: the corresponding elements of corresponding rows and columns are equal. In other words, in a symmetric matrix we have that the element \(x_{ij}\) is equal to \(x_{ji}\).
\[ \left[\begin{array}{ccc} 1 & 2 & 3 \\ 2 & 4 & 5 \\ 3 & 5 & 6 \\ \end{array}\right] \]
2.3.4 Diagonal Matrix
A diagonal matrix is a special case of symmetric matrix in which all nondiagonal elements are 0.
\[ \left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 3 \\ \end{array}\right] \]
In other words, in a symmetric matrix, \(x_{ij} = 0\) for \(i \neq j\). The only elements that may not necessarily be qual to zero are those in the diagonal.
\[ \left[\begin{array}{ccc} x_{11} & 0 & 0 \\ 0 & x_{22} & 0 \\ 0 & 0 & x_{33} \\ \end{array}\right] \]
2.3.5 Scalar Matrix
The scalar matrix is a special type of diagonal matrix in which all the diagonal elements are equal scalars.
\[ \left[\begin{array}{ccc} 5 & 0 & 0 \\ 0 & 5 & 0 \\ 0 & 0 & 5 \\ \end{array}\right] \]
2.3.6 Identity Matrix
The identity matrix is a special case of the scalar matrix in which the diagonal elements are all equal to one. This matrix is typically represented with the letter \(\mathbf{I}\). To indicate the dimensions of this matrix, we typically write it with a subscript for the number of rows (or columns). For example, \(\mathbf{I}_{n}\) represents the identity matrix of dimension \(n \times n\).
\[ \mathbf{I}_{3} = \left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array}\right] \]
In matrix algebra, the identity matrix plays the same role as the number 1 in ordinary or scalar algebra.
2.3.7 Triangular Matrix
A square matrix with only 0’s above or below the diagonal is called a triangular matrix. There are two flavors of this type of matrix: upper triangular and lower triangular.
An upper triangular matrix has zeros below the diagonal.
\[ \left[\begin{array}{ccc} 1 & 2 & 3 \\ 0 & 5 & 6 \\ 0 & 0 & 9 \\ \end{array}\right] \quad \textsf{or} \quad \left[\begin{array}{ccc} 1 & 2 & 3 \\ & 5 & 6 \\ & & 9 \\ \end{array}\right] \]
Conversely, a lower triangular matrix has zeros above the diagonal.
\[ \left[\begin{array}{ccc} 1 & 0 & 0 \\ 4 & 5 & 0 \\ 7 & 8 & 9 \\ \end{array}\right] \quad \textsf{or} \quad \left[\begin{array}{ccc} 1 & & \\ 4 & 5 & \\ 7 & 8 & 9 \\ \end{array}\right] \]
2.3.8 Shapes of Matrices
To summarize the various types of matrices described so far, here’s a diagram depicting their shapes. The general type of matrix is a rectangular matrix which can be divided in three types: vertical or tall (\(n > p\)), square (\(n = p\)), and horizontal or wide (\(n < p\)). Among square matrices, the notion of symmetry plays a special role, and among symmetric matrices, we can say that diagonal ones have the most basic structure.
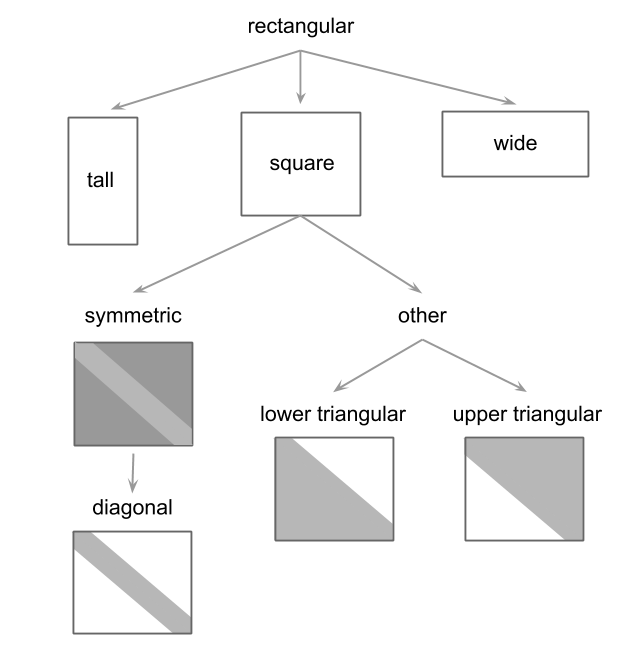
Figure 2.2: Various shapes of matrices
Make a donation
If you find this resource useful, please consider making a one-time donation in any amount. Your support really matters.